« Art Sciences 2025/2026 E3 » : différence entre les versions
Aucun résumé des modifications |
|||
| Ligne 30 : | Ligne 30 : | ||
Matériau : PLA | Matériau : PLA | ||
Densité ρ ≈ 1,24 g/cm3 | Densité ρ ≈ '''1,24 g/cm3''' | ||
Module d’Young E ≈ 3,5 GPa | Module d’Young E ≈ '''3,5 GPa''' | ||
==== Géométrie de la tour ==== | ==== Géométrie de la tour ==== | ||
Hauteur H = 100 cm = 1 m | Hauteur H = 100 cm = '''1 m''' | ||
Base rectangulaire : | Base rectangulaire : | ||
largeur b = 1,7 cm | largeur b = '''1,7 cm''' | ||
profondeur d = 2,5 cm | profondeur d = '''2,5 cm''' | ||
Section A = 1,7 * 2,5 = 4,25 cm2 | Section A = 1,7 * 2,5 = '''4,25 cm2''' | ||
On suppose pour l’instant que la tour est pleine, posée sur une base plane, chargée uniquement par son poids propre. | On suppose pour l’instant que la tour est pleine, posée sur une base plane, chargée uniquement par son poids propre. | ||
| Ligne 50 : | Ligne 50 : | ||
==== Volume ==== | ==== Volume ==== | ||
V = A × H = 4,25 * 100 = 425 cm3 | V = A × H = 4,25 * 100 = '''425 cm3''' | ||
==== Masse ==== | ==== Masse ==== | ||
m = 425 * 1,24 ≈ 527 g | m = 425 * 1,24 ≈ '''527 g''' | ||
==== Poids ==== | ==== Poids ==== | ||
P ≈ 5,2 N | P ≈ '''5,2 N''' | ||
Le poids n’est pas énorme, donc l’écrasement n’est pas un problème. | Le poids n’est pas énorme, donc l’écrasement n’est pas un problème. | ||
| Ligne 66 : | Ligne 66 : | ||
==== Moment d’inertie minimal ==== | ==== Moment d’inertie minimal ==== | ||
I = b*(d^3) /12 = 2,5 * 1,7^3 / 12 ≈ 1,02 cm4 = 1,02×10−8 m4 | I = b*(d^3) /12 = 2,5 * 1,7^3 / 12 ≈ '''1,02 cm4''' = 1,02×10−8 m4 | ||
==== Charge critique d’Euler ==== | ==== Charge critique d’Euler ==== | ||
Pcr = π^2 EI / H2 | Pcr = π^2 EI / H2 | ||
Pcr = (π^2 * 3,5 * 109 * 1,02 * 10−8) / 1^2 = 352 N | Pcr = (π^2 * 3,5 * 109 * 1,02 * 10−8) / 1^2 = '''352 N''' | ||
Ton poids réel ≈ 5 N, donc facteur de sécurité ≈ 70 | Ton poids réel ≈ 5 N, donc facteur de sécurité ≈ 70 | ||
| Ligne 81 : | Ligne 81 : | ||
==== Demi-largeur critique (côté le plus faible) ==== | ==== Demi-largeur critique (côté le plus faible) ==== | ||
1,7 / 2 = 0,85 cm | 1,7 / 2 = '''0,85 cm''' | ||
==== Angle limite avant basculement ==== | ==== Angle limite avant basculement ==== | ||
tan(θ) = 0,85 / 100 -> θ ≈ 0,49∘ | tan(θ) = 0,85 / 100 -> θ ≈ '''0,49∘''' | ||
C’est très faible | C’est très faible | ||
| Ligne 93 : | Ligne 93 : | ||
==== Force appliquée en haut : ==== | ==== Force appliquée en haut : ==== | ||
F = ( P * (b/2) )/ H | F = ( P * (b/2)) / H | ||
F ≈ 15,2 * 0,0085 / 1 ≈ 0,044 N | F ≈ 15,2 * 0,0085 / 1 ≈ '''0,044 N''' | ||
Équivalent à ≈ 4,5 grammes de force | Équivalent à ≈ 4,5 grammes de force | ||
| Ligne 107 : | Ligne 107 : | ||
==== Base nécessaire ==== | ==== Base nécessaire ==== | ||
tan(5∘) = (B/2)/100 -> B ≈ 17,5 cm | tan(5∘) = (B/2)/100 -> B ≈ '''17,5 cm''' | ||
Recommandation réaliste | Recommandation réaliste | ||
socle | socle de 18 × 18 cm minimum | ||
idéalement lourd (PLA plein, ou lesté) | idéalement lourd (PLA plein, ou lesté) | ||
Version du 29 janvier 2026 à 13:25
Cahier n°3 : Champ d'agrainage
Journée du Mardi 27 janvier 2026
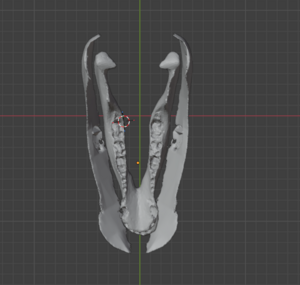
- Nettoyage du scan de mâchoire sur Blender afin d'avoir un modèle propre et imprimable
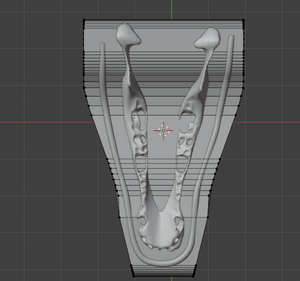
- Création du socle de l’œuvre sur Blender
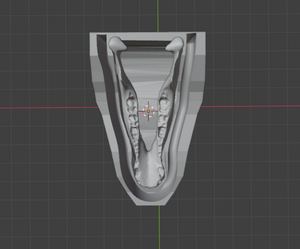
- Début de création du "support/couvercle" qui va entourer la mâchoire sur Blender
- Commande des bobines de filaments bleus
Journée du Mercredi 28 janvier 2026
- Deuxième scan afin d'avoir une mâchoire plus nette à l'aide d'une app -> N'a pas fonctionné, temps de chargement trop long
- Création du socle et finition afin de l'adapter aux attentes du projet sur Blender
Journée du Jeudi 29 janvier 2026
- Amélioration de la coque autour de la mâchoire sur Blender
- Note de calcul afin de déterminer la taille de la plaque de support nécessaire pour éviter le basculement (Voir Note de Calcul n°1)
- Découpage du modèle en 2 pour pouvoir imprimer par impression 3D
Note de calcul n°1
1. Données de départ
Données matériau
Matériau : PLA
Densité ρ ≈ 1,24 g/cm3
Module d’Young E ≈ 3,5 GPa
Géométrie de la tour
Hauteur H = 100 cm = 1 m
Base rectangulaire :
largeur b = 1,7 cm
profondeur d = 2,5 cm
Section A = 1,7 * 2,5 = 4,25 cm2
On suppose pour l’instant que la tour est pleine, posée sur une base plane, chargée uniquement par son poids propre.
2. Poids de la tour
Volume
V = A × H = 4,25 * 100 = 425 cm3
Masse
m = 425 * 1,24 ≈ 527 g
Poids
P ≈ 5,2 N
Le poids n’est pas énorme, donc l’écrasement n’est pas un problème.
Le vrai danger est le flambement (ou le basculement) de la structure.
3. Stabilité au flambement (Euler)
Le flambement se fait autour de l’axe le plus faible → ici le côté 1,7 cm
Moment d’inertie minimal
I = b*(d^3) /12 = 2,5 * 1,7^3 / 12 ≈ 1,02 cm4 = 1,02×10−8 m4
Charge critique d’Euler
Pcr = π^2 EI / H2
Pcr = (π^2 * 3,5 * 109 * 1,02 * 10−8) / 1^2 = 352 N
Ton poids réel ≈ 5 N, donc facteur de sécurité ≈ 70
Pas de flambement en statique.
4. Stabilité au basculement (critique principale)
Le basculement se produit quand le centre de gravité dépasse le bord de la base.
Demi-largeur critique (côté le plus faible)
1,7 / 2 = 0,85 cm
Angle limite avant basculement
tan(θ) = 0,85 / 100 -> θ ≈ 0,49∘
C’est très faible
Une inclinaison minime ou une petite force latérale suffit à la faire tomber.
5. Force latérale maximale admissible
Force appliquée en haut :
F = ( P * (b/2)) / H
F ≈ 15,2 * 0,0085 / 1 ≈ 0,044 N
Équivalent à ≈ 4,5 grammes de force
6. Taille de support recommandée
Pour une stabilité correcte, on vise :
angle critique ≥ 5°
ou force latérale admissible *10 minimum
Base nécessaire
tan(5∘) = (B/2)/100 -> B ≈ 17,5 cm
Recommandation réaliste
socle de 18 × 18 cm minimum
idéalement lourd (PLA plein, ou lesté)
7. Conclusion
Bonne résistance mécanique mais mauvaise stabilité mécanique sans support
Support recommandé : largeur ≥ 18 cm